Paradoja(s)…

Concepto/Ejemplos/Psicología y Mente(O.C.Mimenza)/BBC News(D.Ventura)  —  Una paradoja es una idea, hecho o proposición que contradice la lógica o infringe el sentido común. La palabra paradoja proviene del latín paradoxa, que literalmente quiere decir “contrario a la opinión común”. También se la denomina antilogía. No debe confundirse con los sofismas, que son razonamientos válidos sólo en apariencia.

Son terreno habitual de debate filosófico o lógico, ya que las paradojas suelen conducir a callejones sin salida de la lógica. A menudo se formulan como un modo de transmitir alguna complejidad conceptual en un campo específico del saber, cuya resolución escapa al modo tradicional del pensamiento.

La función de las paradojas es poner de manifiesto algo que ocurre en la vida cotidiana a partir de dos ideas aparentemente opuestas que en algún momento se relacionan.

Suelen utilizarse como una herramienta discursiva y gramatical, son muy funcionales en el plano de la lógica y la discusión de ideas porque llegan a una conclusión inesperada.

En algunos casos, la paradoja puede confundirse con la antítesis. La diferencia entre ambos es que en la antítesis la intención es trazar un plano de diferenciación entre opuestos: en la paradoja los opuestos tienen además una relación de sentido.

– Podemos hablar de los siguientes tipos de paradoja:

• Paradojas verídicas. Aquellas que son verificables, pero que poseen un aire de absurdidad o de contradicción a los propios términos.

• Antinomias. Paradojas cuyo resultado contradice las premisas de las que proviene, a pesar de que sus métodos deductivos son perfectamente válidos.

• Antinomias de definición. De empleo literario mayoritariamente, se basan en definiciones ambiguas, o métodos de pensamiento ilustrativos respecto a un sentido clave.

• Paradojas condicionales. Proposiciones que adquieren un carácter paradójico a medida que se intenta resolverlas, ya sea porque falta información para su resolución o porque ésta simplemente es imposible.

También es usual categorizar las paradojas por el área del saber al que atañen: paradojas matemáticas, paradojas en física, etc.

¿Qué es lo paradójico?

Por extensión, se tilda de paradójico a todas las situaciones, hechos o proposiciones que contienen en su interior una situación irresoluble, irónica, contraria a la lógica o retadora del sentido común.Podemos decir que una situación es paradójica, por ejemplo, cuando en ella nos vemos inmersos en conflictos cuya resolución los empeora, o cuando la persecución de nuestros deseos los torna, justamente, inalcanzables.

Paradojas de la vida

A menudo se habla de las “paradojas de la vida”, para referirse a que frecuentemente las personas nos encontramos en situaciones paradójicas, irónicas o sin solución aparente. En ellas, hacer lo obvio complica todavía más lo que se supone resolvería.

No existe un corpus “oficial” o definitivo de estas paradojas de la vida, sino que se trata de formulaciones populares, dichas por la gente. Se emplean como formas de pensar en la vida y en su arbitrariedad, en la “lógica” propia de la vida, es decir, como una forma de enseñanza respecto a lo que, paradójicamente, no se puede aprender a prever.

Ejemplos de paradojas

• Si quieres paz, prepárate para la guerra. A lo largo de la historia, en muchas ocasiones los procesos que buscaban la paz en una región debieron utilizar la estrategia bélica.

• ¿Qué fue primero, el huevo o la gallina? Las condiciones fundamentales de provenir el uno del otro hacen imposible poner un evento inicial en la secuencia de nacimiento de gallinas.

• No todos los números son expresiones de cuadrados de otros, pero no hay más números que números cuadrados de otros. La infinitud de los números hace que dentro de esos aparezcan subgrupos que a su vez son infinitos.

• El triunfo de la democracia es que vaya mucha gente a votar, precisamente la situación en la que menos vale cada voto. Al aumentar los protagonistas de la democracia, la injerencia individual de cada uno se reduce.

• Por corta que sea una distancia, si uno siempre va recorriendo la mitad de lo que le falta para completarla, nunca llegará. Otra caracterización del infinito, esta vez desde las infinitas particiones.

• ¿Por qué el agua es más barata que los diamantes, siendo que los humanos necesitan agua y no diamantes para sobrevivir? La explicación del valor de la teoría económica clásica sitúa el origen del valor en la utilidad subjetiva y no en la necesidad objetiva.

• ¿Qué sucedería si uno viaja en el tiempo y mata a su abuelo? La posibilidad de viajar en el tiempo hacia el pasado tendría impactos en el presente.

• Si se pudiera viajar en el tiempo hacia el pasado, ya lo sabríamos. La posibilidad de viajar hacia el pasado no tiene en cuenta que el pasado ya se ha vivido.

• Si el universo estuviera poblado por civilizaciones más avanzadas que nosotros, ¿por qué no han venido? Muchas veces se piensa el proceso de encontrar a los demás habitantes del universo como uno que solamente puede hacerse desde la tierra hasta los otros planetas.

• ¿Puede ser verdad la afirmación “solo sé decir mentiras”? Los conjuntos de verdad y mentira se chocan entre sí, poniendo a la afirmación en un gris donde no es ninguna de las dos cosas.

• Aumentar los datos para una estadística puede generar relaciones engañosas. En forma aparentemente contradictoria, no conviene brindar todos los datos sobre una variable pues puede encontrarse una relación que no es tal.

• Si a un hombre se le corta el brazo es un hombre sin brazo. Si se le corta el pie, es un hombre sin pie. Si se le corta la cabeza, ¿qué es? Cuestionamiento a la lógica con la que se asocia la cabeza a la condición de humanidad.

• Es de mala suerte ser supersticioso. Declararse en oposición a la creencia en supersticiones se puede hacer de cualquier modo, menos creando una superstición en base a eso.

• ¿Cómo puede ser que haya bienes que se consuman más cuando sube su precio? La economía se enfrentó a esta paradoja y observó que en algunos casos como ciertos bienes de lujo, una parte de lo que se paga es motivado por lo exageradamente caro de su valor. Si sale más, se comprará más.

• Si bien el ahorro es la fuente de prosperidad, lo es en la medida que no se generalice. Un ahorro generalizado produce una contracción en la economía, que no traerá sino problemas incluso para los que ahorraron.

Algunas célebres paradojas de distintos ámbitos.

– Paradoja de Fermi

Se conoce con este título a la aparente contradicción que existe entre la alta probabilidad de que existan civilizaciones inteligentes en otros planetas y sistemas solares (dadas las dimensiones del Universo) y la total ausencia de evidencias al respecto que tenemos los seres humanos hasta el día de hoy.

Quien primero formuló esta paradoja fue el físico italiano Enrico Fermi, en 1950, en medio de una conversación informal, mientras trabajaba en los Estados Unidos.

Quizá debido al pesimismo que se vivía en aquella época de Guerra Fría y posible conflicto nuclear, Fermi respondió a su propia pregunta que, junto con el desarrollo tecnológico que haría efectivo el viaje espacial, las civilizaciones desarrollaban también el potencial tecnológico para aniquilarse a sí mismas. Así, vaticinaba a la humanidad un futuro nada prometedor.

– Paradoja de Epicuro

También conocida como el Problema del mal, esta paradoja de tipo filosófico o religioso contiene la dificultad que existe para conciliar la existencia del mal, el sufrimiento y la injusticia en el mundo, con la existencia supuesta de una deidad omnisciente y todopoderosa, que además sea benévola, como lo plantea el teísmo clásico.

Esta paradoja plantea básicamente que, si Dios existe y si es omnipotente, omnisciente y además omnibondadoso, si es un Ser Supremo que tiene la capacidad de hacer todo lo que desee, si en realidad conoce al mundo por su sabiduría y poder y que además es sumamente bondadoso con sus hijos, cómo entonces puede ser posible que sea Él quien permita que exista el mal en el mundo.

Estas interrogantes han existido en el mundo desde hace muchos siglos y se relacionan con el problema del mal. Fue Epicuro quien se encargó de formular por primera vez el problema del mal y su resumen puede dividirse entres aseveraciones que dicen de la siguiente manera:

• Si existe una deidad omnisciente, omnipotente y además omnivenevolente, entonces el mal no podría existir.

• La maldad en el mundo sí existe.

• Entonces, esta deidad en realidad no existe.

Estas premisas, si se detallan y analizan desde el punto de vista lógico válido, son ciertas y por tanto la conclusión también debería de serlo. A pesar de ello, no se puede explicar cómo ante la presencia de una deidad todopoderosa puede permitir la existencia del mal.

Esta paradoja encuentra su origen en Epicuro de Samos, un filósofo griego quien fundó en su tiempo la escuela del epicureísmo. El primer hombre que se encargó de analizar desde el punto de vista filosófico el problema del mal.

La formulación de esta paradoja la hizo Epicuro de Samos entre los siglos IV y III a.C. momento en el que expresó y formuló el argumento del mal, lo que tiempo después fue conocida como la paradoja de Epicuro. Su formulación podría parecer un poco lógica pero al mismo tiempo resulta muy contradictoria, especialmente para aquellos que creen en Dios. Para su formulación se basó en tres afirmaciones importantes las cuales también infieren en varias conclusiones lógicas.

Sus premisas entonces se basaron en la existencia de un Dios bueno, que podía estar presente en todos lados al mismo tiempo, que era muy bueno con los seres humanos y que además era poderoso, sin embargo, también profesa la existencia del mal. Entonces, hizo que surgieran varias derivables de la paradoja; si los dioses existen, no tienen la capacidad de poder impedir el mal, si son buenos y quieren detener el mal, no pueden ser omnipotentes y finalmente, el mal existe porque se sufre.

Según el escritor latino y apologista cristiano Lactancio, el filósofo griego Epicuro de Samos fue el primero en formular esta paradoja, razón por la cual a menudo se la menciona con su nombre.

– Paradoja de los gemelos

Llamada también Paradoja de los relojes, se trata de un experimento mental que intenta comprender la diferencia en la percepción del tiempo en dos observadores en estados de movimiento distintos entre sí.

Fue propuesta por Albert Einstein.

Forma parte de lo que hoy conocemos como Teoría de la relatividad especial, en donde el genio físico explica cómo, lejos de ser dimensiones absolutas, el tiempo y el espacio dependen del posicionamiento del observador.

La formulación más usual de esta paradoja se le debe, sin embargo, al físico francés Paul Langevin, y toma como protagonistas a dos gemelos: uno de ellos permanece en la Tierra mientras el otro emprende un largo viaje hacia una estrella lejana, en una nave espacial capaz de alcanzar velocidades semejantes a las de la luz.

Eventualmente, el gemelo viajero regresa y se percata de que es más joven que su hermano en la Tierra, dado que la dilatación del tiempo habría hecho que el suyo transcurriera más lentamente que el tiempo propio de su hermano.

Lo paradójico, sin embargo, surge cuando se hace la observación de que, visto desde la perspectiva del gemelo viajero, es la Tierra la que se aleja a velocidades muy cercanas a la luz, y por lo tanto es su hermano quien tendría que envejecer más lentamente.

Sin embargo, si miramos la situación desde la perspectiva del gemelo que viaja en la nave, quien se está alejando no es él sino el hermano que se queda en la Tierra, con lo que el tiempo debería pasar más lentamente en la Tierra y debería envejecer mucho antes el viajero. Y es aquí donde se encuentra la paradoja.

Aunque es posible resolver esta paradoja con la teoría de la cual surge, no fue hasta la teoría de la relatividad general que la paradoja pudo resolverse con más facilidad. En realidad, en dichas circunstancias el gemelo que envejecería antes sería el de la Tierra: el tiempo pasaría más rápido para este al desplazarse el gemelo que viaja en la nave a velocidades cercanas a la luz, en un medio de transporte con una aceleración determinada.

– Paradoja del viaje en el tiempo

Conocida también como la Paradoja del abuelo, es una paradoja muy popular. Probablemente fue formulada por el escritor de ciencia ficción René Barjael en su novela El viajero imprudente de 1943, aunque otros autores como Mark Twain ya la habían explorado previamente.

La paradoja parte del hecho de que un hombre hace un viaje en el tiempo, regresando al pasado y pudiendo asesinar al padre de su madre, o sea, a su abuelo, antes de que conozca a su abuela y conciba a su madre.

De este modo, su madre no nacería jamás y él mismo, por ende, tampoco, por lo que no podría volver en el tiempo y asesinar a su abuelo, permitiendo entonces que conozca a su abuela y conciba a su madre, quien luego lo concebirá a él, permitiéndole así viajar en el tiempo y asesinar a su abuelo, y así sucesivamente.

– La paradoja de Epiménides (o del cretense)

Una paradoja altamente conocida es la de Epiménides, la cual existe desde la Antigua Grecia y que sirve de base a otras semejantes basadas en el mismo principio. Esta paradoja se basa en la lógica y dice lo siguiente.

Epiménides de Cnosos es un hombre cretense, el cual afirma que todos los cretenses son unos mentirosos. Si esta afirmación es verdadera, entonces Epiménides miente, con lo que no es cierto que todos los cretenses sean mentirosos. Por otro lado si miente no es cierto que los cretenses sean mentirosos, con lo que su afirmación sería verdad lo que a su vez conllevaría que estuviera mintiendo.

– El gato de Scrödinger

Probablemente una de las paradojas más conocidas es la de Scrödinger. Este físico procedente de Austria trataba con su paradoja explicar el funcionamiento de la física cuántica: el momento o función de onda en un sistema. La paradoja es la siguiente:

En una caja opaca disponemos una botella con un gas venenoso y un pequeño dispositivo con elementos radiactivos con probabilidad de un 50% de desintegrarse en un tiempo determinado, y metemos en ella a un gato. Si la partícula radiactiva se desintegra, el dispositivo hará que el veneno se libere y el gato morirá. Dada la probabilidad del 50% de desintegración, una vez pasado el tiempo ¿el gato dentro de la caja, está vivo o muerto?

Este sistema, desde una visión lógica, nos hará pensar que el gato efectivamente puede estar vivo o muerto. Sin embargo, si actuamos en base a la perspectiva de la mecánica cuántica y valoremos el sistema en el momento, el gato está muerto y vivo a la vez, dado que en base a la función de encontraríamos dos estados superpuestos en los que no podemos predecir el resultado final.

Únicamente si procedemos a comprobarlo podremos verlo, algo que rompería el momento y nos abocaría a uno de los dos desenlaces posibles. Así, una de las interpretaciones más populares establece que será la observación del sistema el que provoque que este se modifique, de manera inevitable en la medición de lo observado. El momento o la función de onda colapsa en ese momento.

– La paradoja del abuelo

Siendo atribuida al escritor René Barjavel, la paradoja del abuelo es un ejemplo de la aplicación de este tipo de situaciones al campo de la ciencia ficción, concretamente a lo referente a los viajes en el tiempo. De hecho, a menudo ha sido utilizado como argumento de una posible imposibilidad de viajar en el tiempo.

Esta paradoja establece que si una persona viaja al pasado y eliminara a uno de sus abuelos antes que concibiera a uno de sus padres, la persona en sí no podría llegar a nacer.

Sin embargo, que el sujeto no haya nacido implica que no ha podido cometer el asesinato, algo que a su vez provocaría que sí naciera y pudiera llegara cometerlo. Algo que sin duda generaría que no pudiera nacer, y así sucesivamente.

– Paradoja de la pérdida de información en agujeros negros

Esta paradoja no es especialmente conocida por la mayoría de la población, pero supone un desafío para la física y la ciencia en general aún en la actualidad (aunque Stephen Hawkings propuso una teoría aparentemente viable al respecto). Se basa en el estudio del comportamiento de los agujeros negros e integra elementos de la teoría de la relatividad general y de la mecánica cuántica.

La paradoja se encuentra en que se supone que la información física desaparece por completo en los agujeros negros: se trata de eventos cósmicos que poseen una gravedad tan intensa que ni siquiera la luz es capaz de escapar de ella. Ello implica que ningún tipo de información podría escapar de ellos, de tal manera que termina por desaparecer para siempre.

Se sabe también que los agujeros negros desprenden radiación, una energía que se creía que terminaba por ser destruida por el propio agujero negro y que implicaba también que este se iba haciendo más pequeño, de tal manera que todo lo que se colaba en su interior terminaría por desaparecer junto con él.

Sin embargo esto contraviene la física y mecánica cuántica, según las cuales la información de todo sistema permanece codificado aún si su función de onda llegara a colapsar. Además de ello, la física propone que la materia ni se crea ni se destruye. Ello implica que la existencia y la absorción de la materia por parte de un agujero negro puede llevar a un resultado paradójico con la física cuántica.

Sin embargo, con el paso del tiempo Hawkings corrigió esta paradoja, proponiendo que la información no era en realidad destruida sino que permanecía en los límites del horizonte de sucesos de la frontera espacio-tiempo.

– La paradoja de Abilene

No solo encontramos paradojas dentro del mundo de la física, sino que también es posible encontrar algunas vinculadas a elementos psicológicos y sociales.

Una de ellas es la paradoja de Abilene, propuesta por Harvey.

Según esta paradoja, un matrimonio y los padres de él se encuentran jugando al dominó en una casa de Texas.

El padre del marido propone visitar la ciudad de Abilene, con lo que la nuera coincide pese a ser algo que no le apetece al ser un largo viaje, al considerar que su opinión no coincidirá con la de los demás. El marido responde que le parece bien siempre y cuando a la suegra le parece bien.

Esta última también acepta alegremente. Hacen el viaje, que resulta largo y poco grato para todos.

Al volver uno de ellos insinúa que ha sido un gran viaje. A ello la suegra responde que en realidad hubiese preferido no ir pero aceptó por creer que los demás querían ir. El marido responde que en realidad solo fue para satisfacer a los demás.

Su esposa indica que a ella le ha pasado lo mismo y por el última el suegro refiere que sólo lo propuso por si los demás se estaban aburriendo, aunque no le apetecía realmente.

La paradoja se encuentra en que todos se mostraron de acuerdo en ir a pesar de que en realidad todos hubieran preferido no hacerlo, pero aceptaron a causa de la voluntad de no contravenir la opinión del grupo. Nos habla de conformidad social y el pensamiento grupal, y está relacionado con un fenómeno llamado espiral del silencio.

– Paradoja de Zenón (Aquiles y la tortuga)

 

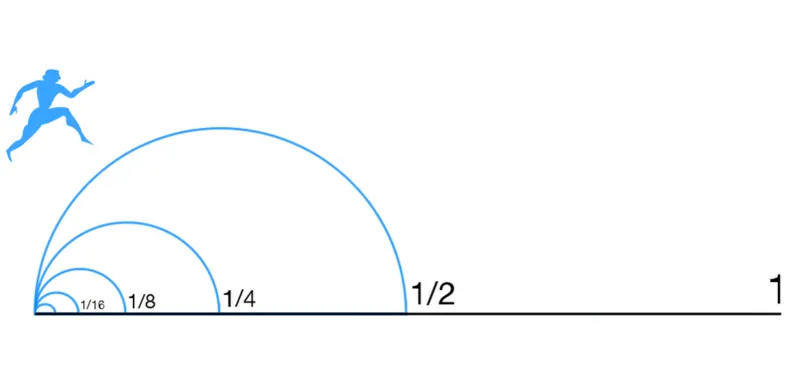
Semejante a la fábula de la liebre y la tortuga, esta paradoja procedente de la Antigüedad nos presenta un intento de demostrar que el movimiento no puede existir.

La paradoja nos presenta a Aquiles, el héroe mitológico apodado “el de los pies veloces”, el cual compite en una carrera con una tortuga. Teniendo en cuenta su velocidad y la lentitud de la tortuga, decide darle una ventaja bastante considerable.

Sin embargo, cuando llega a la posición en la que estaba la tortuga inicialmente, Aquiles observa que esta ha avanzado en el mismo tiempo que él llegaba hasta allí y se encuentra más adelante.

Asimismo, cuando consigue superar esta segunda distancia que los separa la tortuga ha avanzado un poco más, algo que hará que tenga que continuar corriendo para llegar al punto donde ahora está la tortuga.

Y al llegar allí, la tortuga seguirá por delante, pues sigue avanzando sin parar de tal manera que Aquiles siempre se encuentra detrás de ella.

Esta paradoja matemática es altamente contraintuitiva. Técnicamente es fácil de imaginar que Aquiles o cualquier persona acabaría por adelantar a la tortuga relativamente rápido, al ser más veloz.

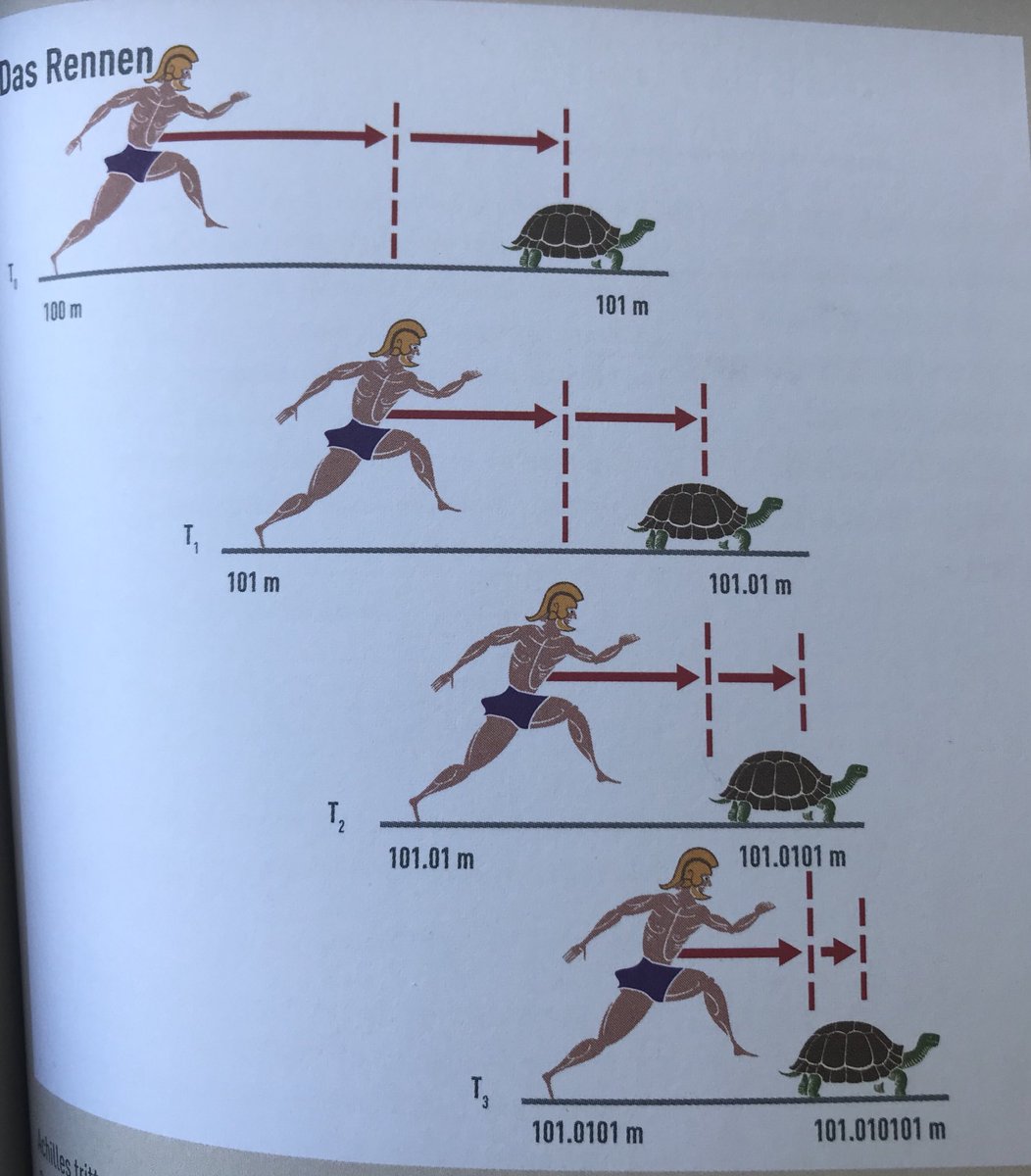
Sin embargo, lo que la paradoja propone es que si la tortuga no para ella seguirá avanzando, de tal manera que cada vez que Aquiles llegue a la posición a la que estaba esta estará un poquito más allá, de manera indefinida (aunque los tiempos serán cada vez más cortos.

Se trata de un cálculo matemático basado en el estudio de las series convergentes. De hecho, aunque pueda parecer sencilla esta paradoja no ha podido ser contrastada hasta hace relativamente poco, con el descubrimiento de la matemática infinitesimal.

– La paradoja sorites

Una poco conocida paradoja pero que sin embargo resulta útil a la hora de tener en cuenta el uso del lenguaje y la existencia de conceptos vagos.

Creada por Eubulides de Mileto, esta paradoja trabaja con la conceptualización del concepto montón.

Concretamente, se propone dilucidar cuánta cantidad de arena se consideraría un montón.

Obviamente un grano de arena no parece un montón de arena. Tampoco dos, o tres. Si a cualquiera de estas cantidades le añadimos un grano más (n+1), seguiremos sin tenerlo.

Si pensamos en miles, seguramente sí consideraremos estar ante un montón. Por otro lado, si a este montón de arena le vamos quitando grano a grano (n-1) tampoco podríamos decir que estamos dejando de tener un montón de arena.

La paradoja se encuentra en la dificultad para hallar en qué punto podemos considerar que estamos ante el concepto “montón” de algo: si tenemos en cuenta todas las consideraciones anteriores un mismo conjunto de granos de arena podría tanto clasificarse como montón como no hacerlo.

– La paradoja de Hempel

Vamos llegando al final de esta lista de las paradojas más importantes con una vinculada al terreno de la lógica y el razonamiento. Concretamente, se trata de la paradoja de Hempel, la cual pretende dar cuenta de los problemas vinculados al uso de la inducción como elemento de conocimiento además de servir como problema a valorar a nivel estadístico.

Así, su existencia en el pasado ha facilitado el estudio de la probabilidad y de metodologías diversas para incrementar la fiabilidad de nuestras observaciones, como las propias del método hipotético-deductivo.

La paradoja en sí, conocida también como la del cuervo, establece que considerar que la afirmación “todos los cuervos son negros” es verdadero implica que “todos los objetos no negros no son cuervos”.

Ello implica que todo lo que veamos que no sea negro y no sea un cuervo reforzará nuestra creencia y confirmará no solo que todo lo no negro no es un cuervo sino también la complementaria: “todos los cuervos son negros”.

Estamos ante un caso en el que la probabilidad de que nuestra hipótesis original sea cierta aumenta cada vez que veamos un caso que no lo confirma.

Sin embargo, hay que tener en cuenta que lo mismo que nos confirmaría que todos los cuervos son negros también nos podría confirmar que son de cualquier otro color, así como el hecho de que únicamente si conociéramos todos los objetos no negros para garantizar que son no cuervos podríamos tener un convencimiento real.

– Paradoja de Teseo