Las matemáticas son, sobre todo, hermosas…

“Me encantan las matemáticas no sólo por sus aplicaciones técnicas, sino sobre todo porque son hermosas”.

The Conversation(M.M.Stadler/M.de León Rodríguez/J.M.Rey) — La matemática Rózsa Péter escribió esta inspiradora frase en su libro Playing with Infinity, dirigido a un público no experto.

Creo que la mayoría de las personas que nos dedicamos profesionalmente a las matemáticas pensamos de esta manera; me refiero a apreciarlas por su belleza. En mi caso, me dedico a la topología, un área preciosa pero muy teórica, así que la parte de las aplicaciones está muy alejada de mis conocimientos y mis intereses.

Sin embargo, actualmente, las matemáticas se valoran precisamente por su gran variedad de aplicaciones en ciencia y tecnología. ¿Es esta percepción la responsable de los grandes cambios en las matrículas de los grados de matemáticas?

– ¿Quién estudia matemáticas?

La Alianza STEAM por el talento femenino, una iniciativa del Ministerio de Educación y Formación Profesional que tiene como objetivo fomentar las vocaciones STEAM en niñas y jóvenes y reducir la brecha de género, publica cada año los datos de la evolución de matriculación en diferentes grados universitarios.

La última actualización, la correspondiente a la gráfica que aparece debajo, describe la evolución y distribución porcentual del alumnado matriculado en el grado de Matemáticas en las universidades públicas españolas entre los cursos académicos 1985/86 a 2022/23.

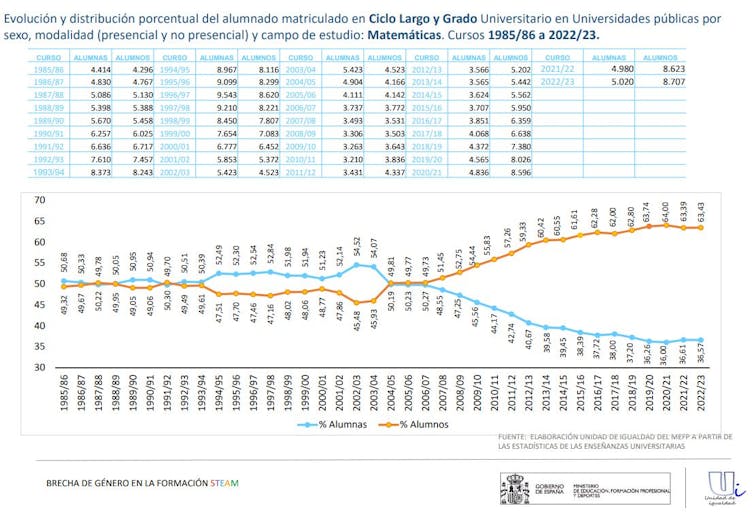
En estos casi 40 años de datos de matriculación en la carrera de Matemáticas, se observa un cambio sorprendente. Hasta el curso 2006/07, la carrera era bastante paritaria, incluso con un mayor porcentaje de alumnas en algunos años (en particular, entre los cursos 1994/95 y 2003/04).

En los primeros años representados en la anterior gráfica, la carrera de Matemáticas tenía salidas profesionales fundamentalmente vinculadas con la docencia. Y la enseñanza es una actividad con una gran presencia de mujeres.

A partir del curso 2006/07, los datos expuestos en la gráfica muestran un cambio de tendencia ininterrumpido. En el último curso analizado, el 2022/23, las mujeres representan tan solo el 36,57 % del alumnado total matriculado en la carrera de Matemáticas.

Si miramos las cifras de matriculación (no sólo la distribución porcentual por sexo), sorprende ver que, en el curso 1987/88, el número de alumnas matriculadas era de 5086 y el de alumnos de 5130. Durante el curso 2022/23, la cantidad de alumnas matriculadas era prácticamente igual a la de 35 años antes, 5020, y la cantidad de alumnos era de 8707.

El curso 1996/97, el de mayor cantidad de estudiantes en la carrera, tenía 9543 chicas y 8620 chicos matriculados. ¿Qué ha ocurrido a lo largo de estos años para que el porcentaje de mujeres y hombres matriculados haya cambiado tanto?

– Las matemáticas interesan a las empresas

Los equipos que trabajan en las empresas son cada vez más multidisciplinares. Dependiendo del tipo de actividad a la que se dediquen, trabajan en ellas conjuntamente especialistas en biología, física, geología, química, matemáticas o distintas ramas de la ingeniería.

Cada persona experta aporta sus conocimientos técnicos y su manera de pensar para resolver los problemas planteados. En las compañías que las contratan, las personas egresadas en matemáticas proponen modelos que simulan situaciones de la vida real, crean algoritmos eficientes o calculan riesgos, entre otras tareas. Son empleos con grandes posibilidades de promoción, con buenas perspectivas de futuro, bien remunerados.

¿Por qué la respuesta ante esta situación tan “favorable” para una persona egresada en matemáticas difiere tanto en el caso de las mujeres y los hombres?

Observando los datos de la evolución en la matriculación en la carrera de Matemáticas, entiendo que los que han cambiado esencialmente su forma de pensar son los chicos: probablemente, en otro momento, habrían elegido estudiar una ingeniería para acceder profesionalmente al ámbito empresarial; ahora optan quizás por las matemáticas por su prestigio, por sus posibilidades de cara al futuro, porque se les dan bien, ¿Por qué les gustan?

Por supuesto que muchas chicas que estudian Matemáticas optan también por salidas profesionales al margen de la enseñanza, pero ¿por qué sus elecciones son tan diferentes a las de los chicos? ¿Por qué ese prestigio que poseen las matemáticas no atrae a las mujeres de la misma manera que a los hombres?

– ¿Importa realmente que no haya paridad en los estudios de matemáticas?

Probablemente muchas personas piensen que no es tan grave, porque los porcentajes en otras disciplinas son peores. Y tienen razón: en el grado de Informática, en el curso 2022/23, las alumnas matriculadas representan el 14,57 % del total de estudiantes. En el grado de Física, en ese mismo curso, solo el 28,44 % del estudiantado es femenino.

Sí, efectivamente, estos datos son peores. Pero entiendo que la evolución en el caso del grado de Matemáticas ha sido especialmente rápido, especialmente sorprendente, especialmente preocupante.

Es una muy mala noticia que cualquiera de estas carreras tenga un porcentaje tan bajo de mujeres entre sus estudiantes. De igual manera que es una mala noticia que los grados en Educación o en Salud y Servicios Sociales tenga un porcentaje tan bajo de hombres entre sus estudiantes.

En un mundo en el que la tecnología juega un papel tan relevante, es una mala noticia que las mujeres no participen en la creación y las decisiones en este campo. Si las matemáticas, la informática o la física “no interesan” a las mujeres en la misma medida que a los hombres, no se trata de un mero asunto de “gustos”. Las preferencias de unas y otros se “moldean” desde edades muy tempranas, y dependen en gran medida de los estereotipos de género. No cortemos las alas ni a las unas ni a los otros.

– Matemáticas, arte y creatividad

“¿Cómo ha encontrado la ecuación de Dirac, profesor Dirac?”

“La encontré hermosa”.

Michael Berry, Paul Dirac: el alma más pura de la física

La 40 ª Conferencia General de la UNESCO proclamó el día 14 de marzo de cada año como Día Internacional de las Matemáticas, fecha elegida porque en el calendario inglés se escribe 3/14, y no hay número más matemático que Pi.

Cada año se selecciona un tema que conecte las matemáticas con otros campos, y este año es Matemáticas, arte y creatividad. Lo que se pretende es hacer una reflexión de lo que une a las matemáticas con el arte, y eso es la creatividad. Pero también la belleza, y en cierta manera la verdad, en cuanto que lo bello y lo verdadero se suelen dar la mano.

– De los cuadros de Da Vinci a los girasoles

Si nos vamos a la antigüedad griega, el canon de belleza era el número áureo, que encontramos en estatuas y monumentos. En el Renacimiento italiano, Luca Pacioli escribió el influyente tratado De divina proportione, ilustrado con grabados en madera realizados por Leonardo da Vinci, sobre el uso de la proporción áurea en el arte.

Pero esta proporción –un número irracional, por cierto–, también aparece de manera asombrosa en la naturaleza, por ejemplo, en la distribución de las semillas de un girasol o en los ángulos de las ramas de una planta. En el caso de la naturaleza, ésta optimiza el crecimiento y eso hace que surja la belleza.

A lo largo de la historia, son muchos los movimientos artísticos que utilizaron conceptos matemáticos para realizar sus obras. Por ejemplo, el movimiento De Stijl que pretendía “establecer un vocabulario visual de formas geométricas elementales comprensibles por todos y adaptables a cualquier disciplina.”

De hecho, cuando vemos un cuadro de Piet Mondrian pensamos en la geometría.

Y si observamos uno de Jackson Pollock, lo que acude a nuestra mente son los fractales o los fenómenos caóticos.

Y qué decir de las maravillosas obras que la artista donostiarra Esther Ferrer ha ido creando basadas en los números primos.

– Las ecuaciones son bellas

Si vamos al bando de los matemáticos, hablaremos de la belleza de las ecuaciones. Su belleza es una garantía de su autenticidad. El físico matemático Paul Dirac decía: “Este resultado es demasiado bello para ser falso; es más importante que las ecuaciones sean bellas a que se ajusten a los experimentos”. Y también: “Si uno trabaja desde el punto de vista de conseguir la belleza en su ecuación, uno está en una línea segura de progreso”.

Cuando los matemáticos desarrollamos nuestro trabajo de investigación, emborronamos muchos papeles y encerados con nuestros intentos de ecuaciones (visite un estudio de un pintor para comparar). Y a veces se produce la magia creativa, el descubrimiento. Entonces, aquello por lo que hemos estado peleando durante meses aparece ante nuestros ojos de una manera clara.

Ese es el momento eureka, que no ha venido de la inspiración divina sino de un intenso trabajo, aunque el gran matemático indio Ramanujan decía que la inspiración le venía de la diosa de su familia, Namagiri Thayar, que ponía las ecuaciones en su mente.

Venga de donde venga, la creatividad es bienvenida y necesaria tanto en el arte como en las matemáticas. Disfrutemos con ella del día de Pi.

– La realidad matemática

La matemática tiene un enorme prestigio entre las ciencias. En buena parte se debe a la naturaleza de las afirmaciones que establece con su método de conocimiento –se llaman teoremas– y que suelen ser verdades lógicas imperecederas sobre una infinidad de casos. Los asertos de la matemática pura existen eternos, libres de contradicción, en el lugar donde habita el infinito. En cierto sentido, proporcionan “la única verdad que podemos obtener”, dijo el polimata francés Henri Poincaré.

Pero el verdadero prestigio de las matemáticas se debe a que proporciona el lenguaje y la propia cultura para las demás ciencias. La capacidad de las matemáticas para describir el mundo mediante números y ecuaciones –su lenguaje–, y de desentrañarlo a través de su método deductivo –su cultura– ha asombrado a los científicos más importantes de la historia, desde Pitágoras a Galileo o Einstein.

Verdad, eternidad, utilidad, belleza… Con esos atributos resulta natural sobresalir entre las disciplinas científicas. Desde que se refirió así a ellas el genio alemán Carl F. Gauss, la matemática es “la reina de las ciencias”.

– Mapas del universo

El ejemplo paradigmático de esa capacidad asombrosa de describir la naturaleza es el análisis matemático del sistema del mundo de Isaac Newton, que cambió la forma de hacer ciencia para siempre.

Newton elaboró un mapa conceptual –en ciencia se llama modelo– para explicar los movimientos conocidos en la naturaleza. En particular, formuló ecuaciones que determinan con precisión exquisita las trayectorias de los cuerpos que interaccionan a distancia mediante fuerzas de atracción. El éxito de su mapa del mundo es tan espectacular que Newton ha sido considerado el segundo personaje más influyente de la historia, por detrás de Mahoma, según el astrofísico Michael H. Hart.

Un modelo –o mapa– es una representación de la realidad. Su mérito reside en su utilidad, que en general juega en contra de su precisión: el mapa de escala 1:1 es el más preciso, y el más inútil también. La misión de un buen mapa es simplificar la realidad. Para ello no hay inconveniente en falsearla, lo que puede resultar tremendamente útil: basta pensar en los resultados que logra un arquitecto considerando que la tierra es plana.

En realidad, detrás de esa consideración terra-planista está uno de los modelos más útiles de las matemáticas, de linealización se llama: en las cercanías de un lugar sobre una superficie suave, ésta se confunde con su plano tangente.

Debajo se puede ver un mapa que resulta familiar y, si se quiere, muy incorrecto.

Parece un disparate representar las provincias españolas rectangulares. Sin embargo, eso permite asimilar fácilmente la ubicación relativa aproximada de todas las comunidades autónomas y provincias españolas. Además, la sencilla geometría del mapa proporciona útiles fórmulas para recordar las provincias por cada comunidad y su disposición relativa aproximada. Así, la de Castilla-La Mancha es CM=1(GU)+2(TO y CU)+2(CR y AB).

Nuestro mapa es sólo aproximado, claro, y sugiere erróneamente que Granada –bien situada entre Málaga y Almería– no tiene frontera con Albacete, que la tiene. Pero su cometido no es resolver esos detalles, sino representar la división administrativa de España y su geografía relativa aproximada. Y lo consigue francamente bien.

Como nuestro mapa, los modelos matemáticos útiles a veces asumen lo que parece un disparate, como que los cuerpos inertes se atraen a distancia. Como nuestro mapa, los modelos matemáticos suelen ser incorrectos: como son simplificaciones, permiten comprender unas cosas y quizá otras no. A pesar de su sensacional éxito, el modelo de Newton también es incorrecto.

Entre otras cosas, no conseguía explicar anomalías detectadas en la órbita de Mercurio y fue corregido por el modelo de gravitación de Einstein a principios del siglo XX.

No hay un mapa completo del mundo que permita integrar todos los fenómenos de la naturaleza conocidos en lo que los físicos llaman la teoría final. Encontrar ese mapa universal es el problema central de la física moderna.

– El universo de los mapas

Durante el siglo XX, el modus operandi matemático de la ciencia amplió su campo de acción al universo de lo social. Inspirados por su éxito en las ciencias naturales y movidos por intentar construir un mundo mejor, muchos matemáticos y científicos de las ramas “duras” se ocuparon en problemas de las ciencias sociales, fundamentalmente de la economía.

Hay por eso muchas analogías entre los modelos matemáticos sociales y las leyes clásicas de la mecánica y otras ramas de la física. La más notable, por su amplio campo de aplicación, es el modelo de la teoría de juegos formulado por el brillante científico John Von Neumann.

Como la teoría de Newton en las ciencias naturales de su tiempo, la teoría matemática de los juegos se ha descrito como la teoría unificadora de las ciencias sociales. Como el modelo de gravitación de Newton, el de la teoría de juegos también pretende describir la dinámica de los cuerpos, pero éstos animados. En particular, trata de determinar el comportamiento de los individuos en un grupo que interaccionan sometidos a las fuerzas que ejercen sus distintas preferencias.

El teorema de Nash –destacado matemático norteamericano– es aquí el equivalente a la solución de las ecuaciones de Newton. La solución de Nash es la clave de bóveda de las matemáticas de las ciencias sociales. Su trascendencia en las ciencias sociales del siglo XX se ha comparado con la de la doble hélice del ADN en las ciencias naturales.

De nuevo, como el mapa de Newton de la gravitación, el de la teoría de juegos produce predicciones que se desvían del comportamiento observado en ciertas situaciones. La economía conductual –un campo entre psicología y economía– proporciona correcciones del modelo estándar de elección y de la teoría de juegos para explicar esas desviaciones.

– Nuestro universo matemático

Después de tres siglos del momento de Newton, la ciencia –mediante su rol en los avances tecnológicos y en nuestra comprensión del mundo– se ha establecido como el verdadero motor del progreso y la civilización. Las matemáticas gobiernan nuestro mundo, y en particular, son un vector importante del crecimiento económico.

En el siglo de los algoritmos, son los mapas matemáticos sus auténticos creadores, y siguen omnipresentes en todas las versiones de nuestra vida cotidiana. El GPS y la geolocalización para nuestra vida física, la ordenación de los buscadores de internet para la virtual, o la fórmula que establece la cuota de nuestra hipoteca para nuestra vida financiera, por poner tres ejemplos, son todos diseños matemáticos como el de Newton.

Ya en el siglo XVII, Galileo pensaba que la naturaleza estaba escrita en matemáticas y es humanamente imposible entenderla sin ellas. En el siglo XXI, la sociedad del conocimiento está también escrita en matemáticas y no parece posible formar parte de ella sin entender mapas matemáticos.

Más allá de que las matemáticas contengan la explicación del universo, el físico Max Tegmark ha propuesto que el propio universo es matemático. Nuestra esencia última sería una estructura matemática. Tendría razón Pitágoras. Ya hace 2 500 años pensaba que, en su nivel más profundo, la realidad es matemática.

nuestras charlas nocturnas.