Génesis de la relatividad general para principiantes…

JotDown(O.Domosti) — En el transcurso de estos primeros diez años de vida de Jot Down se celebró el centenario de la presentación de la teoría de la relatividad general de Albert Einstein. Incluso lo conmemoramos con un pack de trimestrales que llevaban impreso en el lomo su ecuación de campo (Gab = 8 Π G Tab), una fórmula que parece tan inocente y sencilla que da la sensación de que la ecuación de gravitación de Isaac Newton (F = G m1 m2 / d2) es más compleja.

Nada más lejos de la realidad. Llegar a ella fue una tarea titánica de una de las mentes más prodigiosas de la historia de la ciencia. Newton, quitándose importancia, dijo en su momento: «Si he visto más lejos, ha sido encaramándome a los hombros de gigantes».

Siguiendo con la metáfora, cuando Einstein decidió enfrentarse a la generalización de su teoría de la relatividad especial, solo había un circo de tres pistas con gigantes y enanos dispersos, y él se tuvo que encargar de agruparlos, organizarlos para que formaran un castell, montar un andamio sobre ellos y encaramarse hasta la cima para enarbolar una banderita con la ecuación de campo anteriormente grafiada. Solo así consiguió «ver más lejos».

• Matemáticas al poder

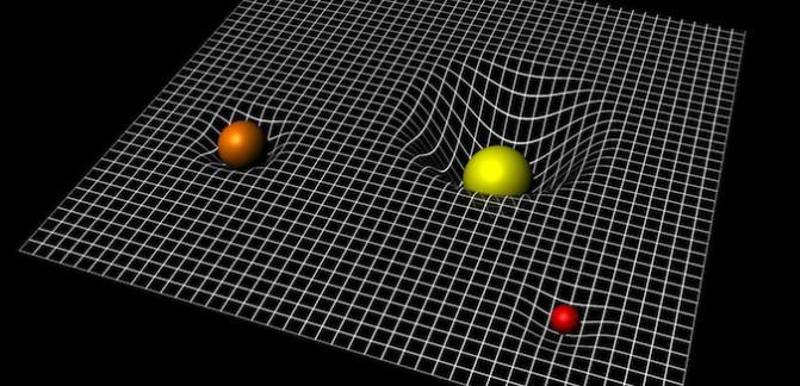
Gracias a las películas de ciencia ficción, forma parte de la cultura popular que la relatividad general consiste, a grandes rasgos, en que el espacio-tiempo se deforma por la presencia de los astros. Una forma simplificada de visualizar este fenómeno es con el consabido juego de pelotas de distintos tamaños y pesos sobre una red o tela tensa.

Quien haya dormido en una cama vieja junto a alguien mucho más pesado incluso lo habrá experimentado en primera persona. Pero describirlo matemáticamente es otra historia, porque la geometría convencional no sirve.

Durante siglos, la representación de la realidad a la que estaba acostumbrado el ser humano en su día a día fue la que estableció Euclides quien, a partir de cinco axiomas, construyó su geometría: la conocida como plana o euclídea. Los axiomas son unas proposiciones de partida que se asumen como ciertas, y durante unos mil quinientos años no hay constancia de que nadie chistara a Euclides.

Hasta que, en el siglo XIX, el quinto axioma («por un punto exterior a una recta se puede trazar una única paralela a la recta dada») fue rebatido por un puñado de matemáticos sensacionales que consiguieron plantear otras geometrías consistentes y que no daban lugar a contradicciones partiendo de una premisa diferente.

En torno a 1823, János Bolyai remató una geometría en donde el quinto axioma de Euclides era falso porque, en la suya, por un punto exterior a una recta hay más de una recta paralela a la primera. Esta geometría se denomina hiperbólica y su «plano», donde se contienen las rectas y puntos, es una seudoesfera que tiene una forma similar a dos campanas de trompa pegadas una a la otra.

Y no era el único resultado sorprendente que arrojaba el análisis, ya que la suma de los ángulos interiores de un triángulo resulta menor de 180 grados.

Maravillado por su creación, János se lo comunicó a su padre, el también matemático Farkas, quien a su vez compartió orgulloso los descubrimientos de su hijo con su antiguo profesor de la Universidad de Gotinga, a quien aún lo unía cierta amistad.

Este antiguo profesor era nada más y nada menos que Carl Friedrich Gauss, uno de los mejores matemáticos de todos los tiempos.

Contra todo pronóstico, aunque Gauss reconoció el talento de János, transmitió algo más de tibieza ante la geometría hiperbólica porque, según manifestó, él la había concebido antes, pero se lo había guardado para evitar jaleos con los seguidores de Euclides radicalizados.

Estas palabras en boca de cualquier otro matemático podrían sonar a machada, pero dado el talento y el bagaje de Gauss, los Bolyai asumieron que decía la verdad.

Esto le sentó a János como un jarro de agua fría, suponemos que volcó algunos muebles por la impotencia, abandonó las matemáticas, ingresó en el ejército y estuvo años sin publicar lo que había descubierto.

Cuando al fin se decidió a darlo a conocer, en 1932, como un apéndice dentro de un libro de su padre, ya era tarde: un matemático ruso llamado Nikolái Lobachevski se le había adelantado. Aunque oficialmente fuera Lobachevski el primero en difundir la geometría hiperbólica, casi siempre va unida su autoría a la de Bolyai y, en menor medida, a Gauss.

Premio de consolación para el pobre János.

A otro alumno de Gauss (el mundo era un pañuelo en el siglo XIX), Bernhard Riemann, también le dio por las geometrías no euclídeas (entre otras muchas cosas, como veremos más adelante, porque estamos ante otro fenómeno de las matemáticas). En su caso, el quinto axioma de Euclides se transformó en «por un punto exterior a una recta no pasa ninguna recta paralela».

Además, los ángulos interiores de un triángulo en esta geometría siempre suman más de 180 grados. Y, por si fuera poco, las rectas no son infinitas (a diferencia de la euclidiana y la hiperbólica). Todo esto se consigue al considerar un elipsoide (por eso se denomina elíptica) como el «plano» donde se encuentran los puntos y las «rectas».

Para visualizarlo, basta con coger un globo sin inflar y dibujar sobre él un triángulo convencional. Cuando hinchamos el globo y se estira la goma, vemos cómo se curvan los lados del triángulo y se abren los ángulos que forman.

Y si consideramos una esfera (un caso particular de un elipsoide), las «rectas» (entendidas como el camino más corto entre dos puntos, denominadas técnicamente geodésicas), siempre son círculos máximos, por lo que es imposible trazar una paralela por un punto exterior sin que corte a la recta inicial y, evidentemente, siempre se cierran (basta con pensar en el ecuador de la Tierra).

Este tipo de geometrías no euclídeas de primeras suenan a pura abstracción, aunque si visualizamos sus «planos» y sus «rectas» vamos comprendiendo las posibles aplicaciones ante el ejemplo de un gordo tumbado en la cama. En efecto, fueron unas herramientas indispensables para que Einstein diera forma a la relatividad general.

Además, sin alejarnos de Gauss y Riemann, hubo otros desarrollos matemáticos esenciales para que se pudiera llegar a la ecuación de campo que plasmamos en el primer párrafo. Si nos dicen que describamos un objeto, en general enumeraremos los aspectos singulares que apreciamos desde fuera.

Por ejemplo, si se trata de un jarrón, diremos que en la parte superior tiene una abertura, que su forma es sensiblemente cilíndrica y que la base está cerrada.

Pero si ante la misma pregunta alguien responde que si se mueve en una dirección determinada vuelve al punto de partida y si se desplaza en una dirección perpendicular a la anterior llega a una abertura o a la base, inmediatamente marcaremos el 112. Algo así fue lo que propuso Gauss.

En lugar de definir las superficies bidimensionales desde un punto de vista tridimensional o exterior, realizó el análisis desde la propia superficie, describiendo su relieve, los valles y las cimas, la curvatura, en definitiva, a medida que se recorre. Riemann cogió el testigo de su profesor en este punto y lo generalizó para cualquier número de dimensiones.

En la conferencia de 1854 donde compartió estas ideas, Riemann concluyó de modo premonitorio: «Esto nos conduce a los dominios de otra ciencia, al ámbito de la física, donde nuestro propósito de hoy no nos permite adentrarnos».

Hubo que esperar más de cincuenta años para retomar el asunto, porque en 1915 Einstein pudo formular su teoría gracias a esta forma de analizar el espacio ideada por Gauss y generalizada por Riemann: describiendo la curvatura del espacio-tiempo desde su interior (además de otras ventajas matemáticas más complejas de describir y que se resumen excelentemente en la página de Wikipedia sobre la geometría de Riemann: «No hay introducción fácil a la geometría de Riemann»).

No obstante, aun disponiendo de estos artificios matemáticos desde hacía décadas, nadie los había usado, ni pensado en que el espacio se deformaba, ni que había más dimensiones que las tres del espacio, ni que la luz hacía cosas raras… Einstein fue el primero al que se le ocurrió. ¿O no?

• En el principio (casi) todo era éter

El ambiente científico del siglo XIX era etéreo, en el sentido de que todo era éter. El comodín que lo resolvía todo. Era imperceptible y no se tenían pruebas físicas de que existiera, pero las teorías se construían o aparentemente funcionaban a partir de la premisa de que en el vacío del espacio todo estaba formado por éter.

Era el soporte de la realidad. Puede sonar ridículo, pero, salvando las distancias, en cierto modo no es muy diferente a lo que sucede ahora con la materia oscura: es algo que la tecnología actual no detecta, pero que según la teoría y ciertas observaciones indirectas se asume que debe estar ahí.

A finales del siglo XIX, Karl Pearson desarrolló la teoría del chorro de éter. «De acuerdo, todo es éter, pero de algún lado debe venir y a algún lado debe marchar», conjeturó. Lo resolvió con una cuarta dimensión: de ella manaba el éter y a ella volvía a través de unos sumideros —¿no les recuerda a los agujeros negros?—. Y no solo eso.

En su libro La gramática de la ciencia especulaba con qué le sucedería en cuanto a la percepción del tiempo a alguien que viajara a la velocidad de la luz. También resulta familiar. Y hay constancia de que Einstein leyó ese libro.

Aún hay más.

El astrónomo Simon Newcomb propuso en 1888 un modelo de éter basado en el espacio hiperdimensional de geometrías no euclídeas y mantuvo correspondencia en la misma época con Charles Sanders Peirce, quien por su parte esbozó una teoría del espacio para explicar «las características del tiempo, el espacio, la materia, la gravedad, etc.», donde hablaba de cuatro dimensiones, de geometría hiperbólica y la realidad del espacio absoluto.

Pero más revolucionarios fueron los estudios del matemático William Kingdon Clifford, que ya en 1870 utilizó la geometría elíptica de Riemann para deducir que la variación de curvatura del espacio era lo que en realidad percibíamos como movimiento del éter y los astros. Para muchos, es el precursor de los conceptos de la relatividad general.

En resumen, antes de Einstein ya había ideas innovadoras, incluso se conocían ciertas herramientas matemáticas avanzadas, pero lo que no se conseguía era articularlas para que reprodujeran correctamente las observaciones.

• El duro camino entre lo especial y lo general

La relatividad especial que se publicó en 1905 supuso un avance colosal en muchos aspectos de la física, pero estaba limitada porque solo contemplaba los efectos bajo velocidad constante: no tenía en cuenta las aceleraciones. Einstein contó posteriormente que, en 1907, pensó en que, cuando un hombre cae libremente, no siente su peso.

Es decir, en determinadas circunstancias, es lo mismo hablar de un objeto que sufre aceleración o que está bajo el efecto de un campo gravitatorio. A partir de este principio de equivalencia y teniendo en cuenta que, según la relatividad especial, la velocidad de la luz es una constante, la primera generalización que esbozó Einstein predecía que los campos gravitatorios afectaban a la propagación de la luz y que los relojes se ralentizan cerca de grandes masas gravitatorias.

Esto sentaba las bases para lanzar una OPA hostil a la gravitación universal de Newton, ya que en esta teoría la atracción gravitatoria no dependía del tiempo, era instantánea, lo que era contrario a la limitación de la velocidad de la luz.

Era la presencia de masas lo que configura el espacio-tiempo, lo deforma, lo curva, y no existe una fuerza invisible e instantánea que ejerza atracción entre los astros. Unas ideas no muy alejadas de lo que algunos habían aventurado a finales del XIX, como hemos visto, pero quedaba el durísimo paso de los conceptos a la formulación.

Aunque se ha extendido la errónea idea de que en el colegio las matemáticas se le daban regular (una confusión en la interpretación de las escalas de calificación), «Einstein era un buen matemático intuitivo y tuvo un poco de problema con estas ideas, pero sabía lo que quería. Cuando vio lo que Riemann había hecho, supo que era eso», contó Roger Penrose, premio nobel de física en 2020, en una entrevista.

No obstante, en un primer momento no estaba tan abierto a esos jaleos matemáticos. En 1907, un antiguo profesor suyo —insisto, el mundo era entonces un pañuelo— de la Escuela Politécnica de Zúrich llamado Hermann Minkowski, definió una métrica para un espacio-tiempo acorde a la relatividad especial, donde lo que se medía no era la separación entre dos posiciones, sino entre dos sucesos.

Minkowski utilizó para ello el análisis de geometría de superficies de dimensión superior que hemos mencionado antes. La primera reacción de Einstein fue furibunda: «Desde que los matemáticos se abalanzaron sobre la teoría de la relatividad, ni yo mismo la entiendo».

Pero en 1912, tras unos años de intenso trabajo, tuvo que reconocer que no había forma de llegar a la relatividad general sin echar mano de las matemáticas avanzadas: «Debes ayudarme o si no me volveré loco», le suplicó al matemático Marcel Grossmann, amigo suyo desde los tiempos en que fueron compañeros de estudios. Grossmann lo introdujo tanto en la geometría elíptica como en el análisis tensorial que se originaba en los trabajos de Gauss y Riemann.

Incluso en 1913 publicaron de forma conjunta el artículo «Esquema de una teoría de la relatividad generalizada y de una teoría de la gravitación», donde expusieron por dónde iban a ir los tiros de la construcción matemática de la relatividad general. La cosa parecía ir sobre ruedas, a pesar del complicado trabajo que aún tenía por delante.

Pero en 1915, con la intuición de que la pancarta de meta estaba cerca, surgió un problema inesperado. Alguien se le podría adelantar.

• Me llamo Hilbert, David Hilbert

En el verano de 1915, Einstein fue invitado por un profesor de la Universidad de Gotinga a dar unas conferencias sobre sus progresos en la teoría de la relatividad general.

Este profesor era David Hilbert, uno de los más grandes matemáticos de su época que, en aquel momento, estaba interesado en las aplicaciones físicas de las matemáticas, tal vez por la influencia de su amigo Minkowski —un pañuelo, sin duda—, y, por tanto, qué mejor forma de hacerlo que escuchar los avances del mayor talento mundial de la física del momento.

Hilbert se sintió fascinado por las implicaciones de la teoría de Einstein en construcción y se vio capacitado para intentar llegar a la formulación final por su cuenta, aunque en comunicación con el físico. 

Durante el mes de noviembre de aquel año intercambiaron numerosas cartas, donde se iban transmitiendo los avances, se aclaraban mutuamente dudas y compartían las dificultades que se iban encontrando. Cuando Einstein finalmente envió su artículo definitivo titulado «Las ecuaciones de campo gravitacional» el 25 de noviembre de ese mismo año, suscitó dudas.

Había quien pensaba que se había aprovechado de la buena fe y los conocimientos del matemático para llegar a buen puerto, e incluso hay quien vio tongo porque Hilbert había enviado antes su artículo con sus propias ecuaciones de campo, pero se lo publicaron más tarde (en marzo de 1916 frente al 2 de diciembre de 1915).

Era un poco extraño que, si se había producido algún plagio o trampa, la relación de Hilbert y Einstein siguiera gozando de una extraordinaria cordialidad. Finalmente, este extremo quedó aclarado en 1997 cuando unos historiadores localizaron en los archivos de la Universidad de Gotinga las primeras pruebas de impresión del artículo de Hilbert.

Además de estar fechadas el 6 de diciembre de 1915, el artículo aún contenía algún error y, sobre todo, carecía de ecuaciones de campo que en el definitivo sí aparecían. Por si fuera poco, en el artículo publicado en marzo de 1916 Hilbert felicitaba indirectamente a Einstein. Pocas dudas.

Hilbert fue un excelente matemático. De su historial, lo que mayor fama pública le ha granjeado sea probablemente el planteamiento de los veintitrés problemas del milenio, alguno aún sin resolver (como la hipótesis de Riemann). Pero sus contribuciones a las dos teorías más importantes de la física del siglo XX fueron también capitales.

Además de sus aportaciones a la relatividad general de Einstein, la habilidad matemática de Hilbert fue utilizada para demostrar que la formulación de ondas de Schrödinger y la matricial de Heisenberg, las piedras angulares de la mecánica cuántica, son análogas. No es mala contribución a la física para solo «un matemático».

En resumen, la densidad de genios de las matemáticas y la física que se produjo en los cien años comprendidos entre 1850 y 1950 no ha tenido parangón en toda la historia. Einstein fue, con pocas dudas, el más brillante de todos ellos, pero su relatividad general fue factible gracias al apoyo y la consulta de los avances que habían logrado otros colegas. 

---

• Bibliografía mínima para saber mucho más y bastante mejor

-Generaciones cuánticas, de Helge Kragh. A finales del siglo XIX se decía que toda la física estaba ya definida, que solo quedaba afinar las mediciones. Y al poco llegó la relatividad y la física cuántica, desbaratando muchas de las ideas preestablecidas. En este denso volumen se realiza un repaso de los avances de los distintos campos de la física y la tecnología que se produjeron durante el siglo XX.

-Cuando las rectas se vuelven curvas: las geometrías no euclídeas, de Joan Gómez i Urgellés. Durante siglos, la geometría que estableció Euclides fue la única válida para la representación de nuestra realidad, hasta que lo que parecían concepciones abstractas de algunos matemáticos como Gauss, Riemann, Lobachevski y Bolyai se demostraron necesarias para describir el mundo físico que nos rodea. Una buena introducción a las bases de esas geometrías no euclídeas.

-Lo que no podemos saber, de Marcus du Sautoy. El famoso autor de La música de los números primos expone en esta obra los límites actuales del conocimiento humano, describiendo cómo se llegó a las teorías físicas vigentes en la actualidad y cuál es su campo de validez.

-Einstein. El espacio es una cuestión de tiempo, de David Blanco Laserna. Una gran introducción a la teoría de la relatividad con incisos descriptivos de otros científicos y la época.

nuestras charlas nocturnas.